目次
  1. 概要: LLM学習過程から得る学びの共有
  2. DeepSeek-R1とは
  3. DeepSeek-R1モデルの学習戦略
  4. 補足情報
  5. 今後のMIプラットフォームへの示唆
  6. まとめ
  7. 参考文献

概要: LLM学習過程から得る学びの共有

この記事は、2025年1月20日に公開された大規模言語モデルDeepSeek-R1の学習戦略をまとめたものになります。

この規模のLLMの学習過程の詳細が公開されることは最近では珍しいです。実際にOpenAI o1などはどのように作られたか一切公開されておらず、どのような学習戦略のもと学習されたのか推測する論文が多数発表されていたりします。(例: Macro-o1)

DeepSeek-R1の作り方の情報は化学タスクに強いLLMを作る際にも役立つと考えています。公開して間もない情報をもとにまとめているものですので、間違いなどありましたらコメントお願いします。

LLMの記事および材料分野の研究開発における応用については過去の記事をご参照ください。

LLMの基礎を読む
LLM活用事例を読む

DeepSeek-R1とは

DeepSeek-R1は、推論能力の向上を目的として設計されたLLMであり、その学習戦略は多段階の強化学習（Reinforcement Learning; RL）と教師ありファインチューニング（Supervised Fine-Tuning; SFT）に基づいています。特筆すべきは、RLのみで学習を行ったDeepSeek-R1-Zeroと比較し、冷スタート（Cold Start）や再学習を活用することで小さい初期データからのパフォーマンスを大幅に向上させた点です（図1）。

以下では、DeepSeek-R1の学習戦略について簡単に紹介します。

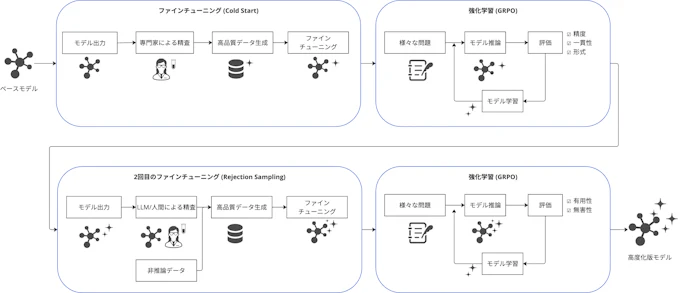
ベースLLM出力を基に教師あり学習とGRPOによる強化学習を2回繰り返し、精度・一貫性・有用性を向上させるDeepSeek-R1モデル構築スキーム。化学や材料科学などに特化させた高品質な推論能力を持つ高度化モデルを生成可能

図1. DeepSeek-R1モデルの学習スキームの概略図（出所: miLab編集部作成）

DeepSeek-R1モデルの学習戦略

DeepSeek-R1ではDeepSeek-V3をベースとして、教師あり学習と強化学習を2回繰り返すことで、初期の学習データがあまりないところからモデルの性能を大幅に向上させることに成功しています。

Cold Start: 初期データの教師ありファインチューン

前モデルのDeepSeek-R1 Zeroではこの段階を踏まずに強化学習を開始していますが、開始直後の推論が不安定になるなどの問題がありました。これを回避するためにR1ではまず少量のデータを用いたファインチューンを行っています。
用いるデータは主にDeepSeek-R1 Zeroの出力を人間が修正するなどの方法を通じて取得された品質の高い推論の出力例です。これらをまず学習させることにより、強化学習の初期フェーズを安定させることができます。

Reasoning-oriented Reinforcement Learning: 1回目の強化学習

この強化学習ではGroup Relative Policy Optimization(GRPO) と呼ばれるコスト関数を用いています。これは問題に対するLLMの回答を複数出力させてそのグループでの評価を用いて強化学習を行う手法です。

$$ \mathcal{J}_{GRPO}(\theta) = \mathbb{E} \left[ q \sim P(Q), \{o_i\}_{i=1}^{G} \sim \pi_{\theta_{\text{old}}}(O|q) \right] \\ \left[\frac{1}{G}\sum_{i=1}^{G} \left( \min \left(\frac{\pi_{\theta}(o_i|q)}{\pi_{\theta_{\text{old}}}(o_i|q)} A_i, \text{clip}\left(\frac{\pi_{\theta}(o_i|q)}{\pi_{\theta_{\text{old}}}(o_i|q)}, 1-\epsilon, 1+\epsilon \right) A_i\right)- \beta \mathcal{D}_{KL}(\pi_{\theta} || \pi_{\text{ref}})\right)\right], $$

$$ \mathcal{D}_{KL}(\pi_{\theta} || \pi_{\text{ref}}) = \frac{\pi_{\text{ref}}(o_i|q)}{\pi_{\theta}(o_i|q)} - \log \frac{\pi_{\text{ref}}(o_i|q)}{\pi_{\theta}(o_i|q)} - 1, $$

強化学習を行うための報酬は主に出された数学の問題に対する答えや、出力されたプログラムを走らせた場合の結果などを用いてルールベースに決められます。さらに、出力の精度だけでなく、途中の思考のための出力を<think><\think>タグで挟むように強制する形式報酬や思考のための出力に複数の言語を含まないことによる一貫性報酬が報酬として与えられます。一貫性報酬は思考のための出力が複数の言語が混じった状態でなされる問題を回避するために考案されました。

この強化学習により、推論能力を向上させていきます。

Rejection Sampling and Supervised Fine-Tuning: 2回目の教師ありファインチューン

強化学習を一通り終えたのち、この時点での学習済みモデルを用いて教師データを作成します。このために、まず推論プロンプトを与えてモデルに推論の過程を出力させます。これらの出力を人間もしくは他のLLM(この研究ではDeepSeek V3のパイプラインを利用）で選別と改変を行うことで品質の良い推論過程のデータを作成します。
さらにこれに一般的なQAなどの非推論データも加えて学習させます。この時、一部のデータに関してはDeepSeek V3を用いて推論過程を生成させてデータに付け加えます。

Reinforcement Learning for all Scenarios: 2回目の強化学習

1回目と同様のルールベースによる成果報酬に加えて、人間にとっての好ましさを報酬として与えています。これは有用性と無害性の観点で出力をDeepSeek V3に評価させてその得点を報酬としています。

補足情報

小規模モデルの学習比較

Qwen-32Bを用いて同様の強化学習戦略を用いて学習させた場合と、DeepSeek-R1のデータを学習させた場合（蒸留と呼ばれる)では、蒸留を用いたモデルの方が強化学習戦略を用いた場合よりもパフォーマンスが向上しました。小規模なモデルを向上させるには1から強化学習させるよりも大規模なモデルのデータを学習させた方が有利なようです。

アルゴリズムの試行錯誤

プロセス報酬モデル

推論ステップ一つひとつに対して報酬を与える強化学習手法です。推論ステップを明確に分離するのが困難なこと、推論ステップを評価するモデルを作成するために追加のトレーニングデータが必要なことから、投入するリソースに対して費用対効果が低いと結論されています。

モンテカルロ木探索(MCTS)

推論ステップを細かく分けて木構造を作り、モデルが解空間を体系的に探索できるようにする手法です。事前学習済みの価値モデルを用いて探索をガイドします。

 LLMの推論に用いるには

  1. 探索空間が膨大になりすぎるため制限が必要
  2. 価値モデルを段階的に改善することが困難

という2つの問題があり、パフォーマンスを向上させるために使うことは難しかったようです。囲碁のAlphaGoで有名になったMCTSアルゴリズムですが、明確なルールや目標が定義できるゲームや分子生成とは異なり、LLMの推論ではまだ課題があります。

分子生成の記事を読む

今後のMIプラットフォームへの示唆

上述のとおり、人間により精選された高品質データを用いて初期の教師ありファインチューニングを行うことで、初期学習を安定化させ、またその後のモデル学習効率を高めることが示されました。これは、高い専門性をもつ研究者が、組織の研究開発基盤としてのAIモデルないしMIプラットフォームの品質に大きく貢献することを示しています。このような技術は、研究者の専門知識をスケールさせ、組織全体でより大きな成果を生み出すための環境としてのAI・MI活用の可能性を広げるものだと感じます。

研究開発DXの記事を読む

まとめ

DeepSeek-R1は、教師ありファインチューニングと強化学習を組み合わせた学習戦略によって、少量のデータからでも高度な推論能力を実現するモデルの構築に成功しました。この成果は、研究開発や特定の専門分野におけるAI活用の新たな可能性を示唆しています。

参考文献