はじめに
前回の記事『失敗を考慮したベイズ最適化』では、失敗を伴う状況下で行うベイズ最適化手法について基礎的な解説をしました。この記事ではその発展的な例として、研究論文の内容からアルゴリズムの解説を行います。
今回の記事で扱う論文は『Failure-Aware Gaussian Process Optimization with Regret Bounds』です。この表題を邦訳すると『リグレット上界を伴う失敗を考慮したガウス過程最適化』となります。この論文は機械学習分野のトップカンファレンスのひとつ『NeurIPS 2023』に筆者を含むMI-6 Machine Learning Researchチームが投稿して採択されたものです。
この記事ではまず、論文の概説を述べます。次に、論文で提案した失敗を考慮したベイズ最適化の新しいアルゴリズムについて、その挙動を解説します。
論文の概説
ブラックボックス最適化における実用上の重要な課題のひとつに、目的関数の観測が失敗するケースがあります。マテリアルズ・インフォマティクスによる材料開発の現場においても、材料実験の失敗を考慮する必要があります。
これまでは、失敗の考慮は経験則的に対応することが行われており、理論的背景が明確に示された手法は存在しませんでした。従来手法では、失敗が滑らかな単一の潜在関数により引き起こされると仮定したモデル化がなされてきましたが、現実の失敗は複数の未知の要因が絡み合うケースが多く、こうした滑らかなモデルでの記述は不適切となる場合があります。この論文では、こうした実用上の限界を踏まえ、明示的な失敗関数モデルを前提にしないベイズ最適化アルゴリズムを定式化し、この問題において性能保証(リグレット上界)を初めて証明しました。
理論的裏付けが示されたことで、今後は実用的な応用面において、失敗を考慮したベイズ最適化アルゴリズムが扱いやすくなるでしょう。
論文で提案したアルゴリズムの解説
この論文で提案したアルゴリズムは「失敗を考慮したガウス過程上側信頼限界(F-GP-UCB)」と呼びます。F-GP-UCBは、過去の観測結果をもとに、目的関数の最大値が得られる可能性が高い領域を探索しながら、失敗が起こりやすい領域を避けるように設計されています。(ここでの問題設定は目的関数の最大化であると仮定します。)
探索と活用のバランスについては、ベイズ最適化においてよく使われるUpper Confidence Bound (UCB)を獲得関数としてもちいます。各点における目的関数の値の期待値と不確実性を評価し、UCBが最大となる点を次の候補点として選択します。
F-GP-UCBはどのように失敗を回避するのでしょうか?
次の候補点を選ぶ際に、過去の観測で失敗した点を中心とした一定の範囲を探索対象から除外することで、失敗を避けながら探索を行います。ここで、F-GP-UCBの設計で一番のポイントとなるのが、ベイズ最適化のサイクルが進むにつれて、除外領域が徐々に小さくなることです。
この設計のメリットとしては、広い失敗領域の中に狭い成功領域があるようなケースにおいても、サイクル数を十分回すことで、目的関数の最大値を観測することが可能です。これを示したのが図1です。
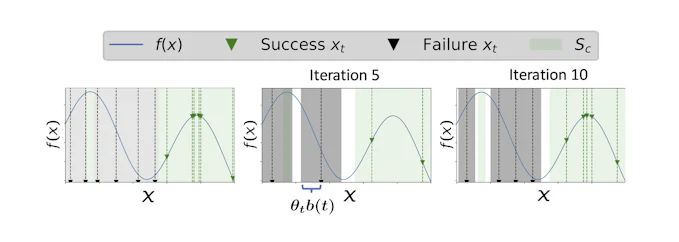
図1. 提案手法の挙動イメージ
まずは実験設定を確認します。
図1の左は、最適化対象となる目的関数と成功・失敗領域を図示したものです。目的関数は青線、成功領域は薄い緑、失敗領域は薄い灰色で示しています。左側の広い失敗領域の中に狭い成功領域があります。目的関数の最大値はこの狭い成功領域の中にあります。
それではF-GP-UCBアルゴリズムの実際の挙動を見ていきましょう。
図1の中央はベイズ最適化の5サイクル目のときの様子です。過去の観測で失敗した点の付近の除外領域を濃い灰色で示しています。このときは、除外領域が大きく、左側の目的関数が最大となる点も除外されています。まだこの時点では最大値を観測することはできません。
図1の右はベイズ最適化の10サイクル目のときの様子です。サイクルが進んだことで、各点の除外領域が狭くなっています。これにより、左側の目的関数が最大となる点も除外領域から外れています。今後サイクルをさらに進めることで、最大値を観測することが可能です。
除外範囲の調整方法について
除外範囲はどのように調整するのでしょうか?
F-GP-UCBは除外領域を事前に定めたスピードで縮小します。論文ではこの縮小スピードを適切に設計することで最終的なアルゴリズムの収束を担保しています。またさらなる発展として、除外範囲をモデルに基づいて適応的に小さくすることも提案しています。具体的には候補点を実際に観測した結果、その不確実性が連続で低くなっていた場合、除外領域の縮小スピードをより速くします。これにより、最大値を含む領域をより早く探索することが可能となります。
このような設計によって、たとえ目的関数の最大値が広い失敗領域に囲まれていたとしても、時間をかけてその局所領域を再び探索可能な状態に戻すことができます。これは、従来の確率的分類モデルに依存した除外戦略では困難だった点でした。
まとめ
今回紹介した論文では、観測の失敗を考慮した新しいベイズ最適化アルゴリズムであるF-GP-UCBについて解説しました。F-GP-UCBは、失敗領域を回避しながら、効率的に最適解を探索することができます。過去の観測で失敗した点の周辺を探索の除外領域とし、除外領域をうまくコントロールすることで、効率的に最適解にたどり着きます。また、この論文において、このアルゴリズムが最適解に収束することも理論的に証明しました。
失敗を考慮したベイズ最適化アルゴリズムは材料開発、機械学習、ロボティクスなど、様々な分野に応用することができます。現実世界の複雑な最適化問題を解決するための強力なツールとなることが期待されます。



























